NUMBER SYSTEM CONVERSION

NUMBER BASE CONVERSION

                   In our previous section, we learned different types of number systems such as binary, decimal, octal, and hexadecimal. In this part of the tutorial, we will learn how we can change a number from one number system to another number system.

As, we have four types of number systems so each one can be converted into the remaining three systems. There are the following conversions possible in Number System

1. Binary to other Number Systems.
2. Decimal to other Number Systems.
3. Octal to other Number Systems.
4. Hexadecimal to other Number Systems.                                                                                                                                                                                                                       

             1.BINARY NUMBER SYSTEM CONVERSION 

Number System with base value 2 is termed as Binary number system. It uses 2 digits i.e. 0 and 1 for the creation of numbers. The numbers formed using these two digits are termed as Binary Numbers. Binary number system is very useful in electronic devices and computer systems because it can be easily performed using just two states ON and OFF i.e. 0 and 1. 

Decimal Numbers 0-9 are represented in binary as: 0, 1, 10, 11, 100, 101, 110, 111, 1000, and 1001 

 

       *BINARY NUMBER SYSTEM TO DECIMAL NUMBER  SYSTEM;    

Binary numbers are represented in base 2 but the decimal numbers are of base 10. Hence, to convert the binary number into a decimal number, the base of that number is to be changed. Follow the steps given below:

• Step 1: Multiply each digit of the Binary number with the place value of that digit, starting from right to left i.e. from LSB to MSB. 
• Step 2: Add the result of this multiplication and the decimal number will be formed.                                                                                                                                              

      *BINARY NUMBER SYSTEM TO OCTAL NUMBER      SYSTEM;

                      Binary numbers are represented in base 2 but the octal numbers are of base 8. Hence, to convert the binary number into octal number, the base of that number is to be changed. Follow the steps given below:

• Step 1: Divide the binary number into groups of three digits starting from right to left i.e. from LSB to MSB.
• Step 2: Convert these groups into equivalent octal digits.

EXAMPLE; To convert (11101011)2 into an octal number

   *BINARY NUMBER SYSTEM TO HEXADECIMAL 

NUMBER SYSTEM;   

Binary numbers are represented in base 2 but the Hexadecimal numbers are of base 10. Hence, to convert the binary number into Hex number, the base of that number is to be changed. Follow the steps given below:

• Step 1: Divide the binary number into groups of four digits starting from right to left i.e. from LSB to MSB.
• Step 2: Convert these groups into equivalent hex digits.

EXAMPLE; To convert (1110101101101)2 into a hex number

 

         2.DECIMAL NUMBER SYSTEM CONVERSION

Number system with base value 10 is termed as Decimal number system. It uses 10 digits i.e. 0-9 for the creation of numbers. Here, each digit in the number is at a specific place with place value a product of different powers of 10. Here, the place value is termed from right to left as first place value called units, second to the left as Tens, so on Hundreds, Thousands, etc. Here, units has the place value as 100, tens has the place value as 101, hundreds as 102, thousands as 103, and so on.  

   * DECIMAL NUMBER SYSTEM TO BINARY NUMBER    SYSTEM;

Decimal numbers are represented in base 10, but the binary numbers are of base 2. Hence, to convert a decimal number to binary number, the base of that number is to be changed. Follow the steps given below:

• Step 1: Divide the Decimal Number with the base of the number system to be converted to. Here the conversion is to binary, hence the divisor will be 2. 
• Step 2: The remainder obtained from the division will become the least significant digit of the new number.
• Step 3: The quotient obtained from the division will become the next dividend and will be divided by base i.e. 2.
• Step 4: The remainder obtained will become the second least significant digit i.e. it will be added in the left of the previously obtained digit.                                                                         After all the iterations are over, the last obtained remainder will be termed as the Most Significant digit.                                                                                                            EXAMPLE;

•  

  *DECIMAL NUMBER SYSTEM TO OCTAL NUMBER      SYSTEM;

Octal Numbers are represented in base 8. Hence, to convert a decimal number to octal number, the base of that number is to be changed. Follow the steps given below:

• Step 1: Divide the Decimal Number with the base of the number system to be converted to. Here the conversion is to octal, hence the divisor will be 8. 
• Step 2: The remainder obtained from the division will become the least significant digit of the new number.
• Step 3: The quotient obtained from the division will become the next dividend and will be divided by base i.e. 8.
• Step 4: The remainder obtained will become the second least significant digit i.e. it will be added in the left of the previously obtained digit.                                                                                                                                                                             EXAMPLE;                                                                     

 *DECIMAL NUMBER SYSTEM TO HEXADECIMAL NUMBER SYSTEM;

Hexadecimal Numbers are represented in base 16. Hence, to convert a decimal number to hexadecimal number, the base of that number is to be changed. Follow the steps given below:

• Step 1: Divide the Decimal Number with the base of the number system to be converted to. Here the conversion is to Hex hence the divisor will be 16. 
• Step 2: The remainder obtained from the division will become the least significant digit of the new number.
• Step 3: The quotient obtained from the division will become the next dividend and will be divided by base i.e. 16.
• Step 4: The remainder obtained will become the second least significant digit i.e. it will be added in the left of the previously obtained digit.                                                                                                                                                                              EXAMPLE;

• 

 

           3.OCTAL NUMBER SYSTEM CONVERSION

Octal Number System is one in which the base value is 8. It uses 8 digits i.e. 0-7 for creation of Octal Numbers. Octal Numbers can be converted to Decimal value by multiplying each digit with the place value and then adding the result. Here the place values are 80, 81, and 82. Octal Numbers are useful for the representation of UTF8 Numbers. 

*OCTAL NUMBER SYSTEM TO BINARY NUMBER SYSTEM;

Octal numbers are represented in base 8, but the binary numbers are of base 2. Hence, to convert an octal number to a binary number, the base of that number is to be changed. Follow the steps given below:

• Step 1: Write each digit of the octal number separately.
• Step 2: Convert each digit into an equivalent group of three binary digits.
• Step 3: Combine these groups to form the whole binary number.

Example: (247)8 is to be converted to binary

*OCTAL NUMBER SYSTEM TO DECIMAL NUMBER SYSTEM;

                   Octal numbers are represented in base 8, but the decimal numbers are of base 10. Hence, to convert an octal number to a decimal number, the base of that number is to be changed. Follow the steps given below:

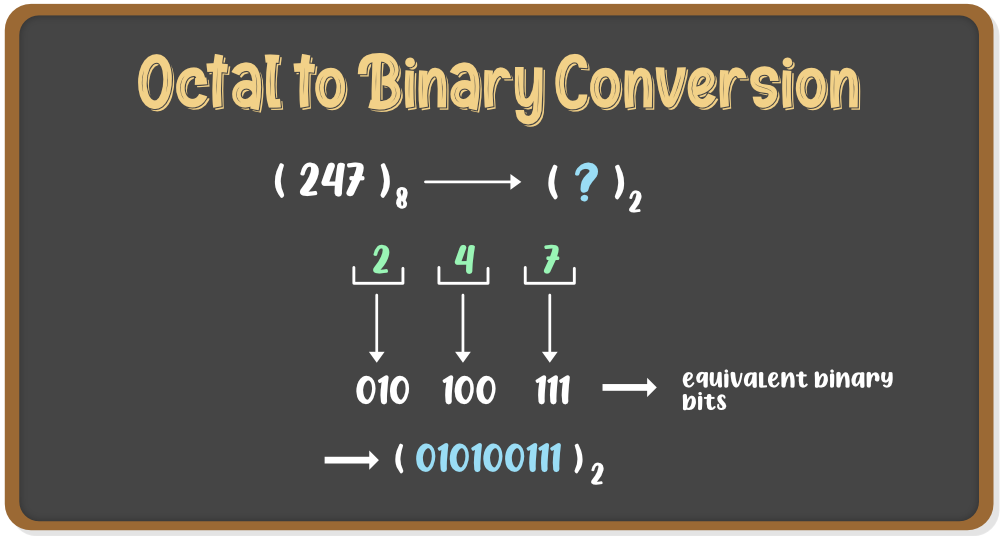
• Step 1: Multiply each digit of the Octal number with the place value of that digit, starting from right to left i.e. from LSB to MSB.
• Step 2: Add the result of this multiplication and the decimal number will be formed.

Example: 

* OCTAL NUMBER SYSTEM TO HEXADECIMAL NUMBER SYSTEM;

Octal numbers are represented in base 8, but the hexadecimal numbers are of base 16. Hence, to convert an octal number to a hex number, the base of that number is to be changed. Follow the steps given below:

• Step 1: We need to convert the Octal number to Binary first. For that, follow the steps given in the above conversion.
• Step 2: Now to convert the binary number to Hex number, divide the binary digits into groups of four digits starting from right to left i.e. from LSB to MSB. 
• Step 3: Add zeros prior to MSB to make it a proper group of four digits(if required)
• Step 4: Now convert these groups into their relevant decimal values.
• Step 5: For values from 10-15, convert it into Hex symbols i.e from A-F                                                                                                                                        EXAMPLE; (5456)8 is to be converted to hex

           4.HEXADECIMAL NUMBER CONVERSION

Number System with base value 16 is termed as Hexadecimal Number System. It uses 16 digits for the creation of its numbers. Digits from 0-9 are taken like the digits in the decimal number system but the digits from 10-15 are represented as A-F i.e. 10 is represented as A, 11 as B, 12 as C, 13 as D, 14 as E, and 15 as F. Hexadecimal Numbers are useful for handling memory address locations.

*HEXADECIMAL NUMBER SYSTEM TO BINARY NUMBER SYSTEM;

Hex numbers are represented in base 16, but the binary numbers are of base 2. Hence, to convert a hexadecimal number to a binary number, the base of that number is to be changed. Follow the steps given below:

• Step 1: Convert the Hex symbols into its equivalent decimal values.
• Step 2: Write each digit of the Hexadecimal number separately.
• Step 3: Convert each digit into an equivalent group of four binary digits.
• Step 4: Combine these groups to form the whole binary number.

EXAMPLE: (B2E)16 is to be converted to binary

*HEXADECIMAL NUMBER SYSTEM TO DECIMAL NUMBER SYSTEM;

Hexadecimal numbers are represented in base 16 but the decimal numbers are of base 10. Hence, to convert a hexadecimal number to a decimal number, the base of that number is to be changed. Follow the steps given below:

• Step 1: Write the decimal values of the symbols used in the Hex number i.e. from A-F
• Step 2: Multiply each digit of the Hex number with its place value. starting from right to left i.e. LSB to MSB.
• Step 3: Add the result of multiplications and the final sum will be the decimal number.

Example: To convert (8EB4)16 into a decimal value

*HEXADEIMAL NUMBER SYSTEM TO OCTAL NUMBER SYSTEM;

Hexadecimal numbers are represented in base 16, but the octal numbers are of base 8. Hence, to convert a hex number to an octal number, the base of that number is to be changed. Follow the steps given below:

• Step 1: We need to convert the Hexadecimal number to Binary first. For that, follow the steps given in the above conversion.
• Step 2: Now to convert the binary number to Octal number, divide the binary digits into groups of three digits starting from right to left i.e. from LSB to MSB. 
• Step 3: Add zeros prior to MSB to make it a proper group of three digits(if required)
• Step 4: Now convert these groups into their relevant decimal values.

Example: (B2E)16 is to be converted to hex

                                                   MORE DETAILS;