SEQUENTIAL GATES
INTRODUCTION;
A Sequential logic circuits is a form of the binary circuit; its design employs one or more inputs and one or more outputs, whose states are related to some definite rules that depend on previous states. Both the inputs and outputs can reach either of the two states: logic 0 (low) or logic 1 (high). In these circuits, their output depends, not only on the combination of the logic states at its inputs but moreover on the logic states that existed previously. In other words, their output depends on a SEQUENCE of the events occurring at the circuit inputs. Examples of such circuits include clocks, flip-flops, bi-stables, counters, memories, and registers. The actions of the circuits depend on the range of basic sub-circuits.
SEQUENTIONAL LOGIC CIRCUIT;
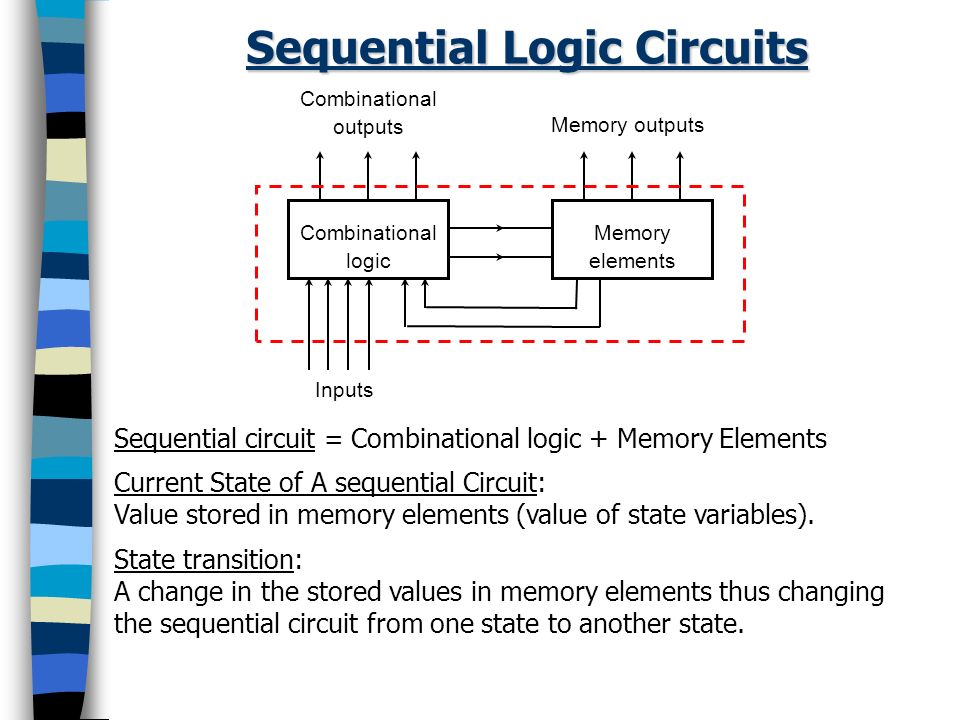
Sequential Logic Circuits use flUnlike Combinational Logic circuits that change state depending upon the actual signals being applied to their inputs at that time, Sequential Logic circuits have some form of inherent “Memory” built in.
This means that sequential logic circuits are able to take into account their previous input state as well as those actually present, a sort of “before” and “after” effect is involved with sequential circuits.
In other words, the output state of a “sequential logic circuit” is a function of the following three states, the “present input”, the “past input” and/or the “past output”. Sequential Logic circuits remember these conditions and stay fixed in their current state until the next clock signal changes one of the states, giving sequential logic circuits “Memory”.
Sequential logic circuits are generally termed as two state or Bistable devices which can have their output or outputs set in one of two basic states, a logic level “1” or a logic level “0” and will remain “latched” (hence the name latch) indefinitely in this current state or condition until some other input trigger pulse or signal is applied which will cause the bistable to change its state once again.
DESIGN PROCEDURE OF SEQUENTIAL LOGIC CIRCUIT;
- This procedure involves the following steps
- First, derive the state diagram
- Take as the state table or an equivalence representation, such as a state diagram.
- The number of states may be reduced by the state reduction technique
- Verify the number of flip-flops needed
- Choose the type of flip-flops to be used
- Derive excitation equations
- Using the map or some other simplification method, derive the output function and the flip-flop input functions.
- Draw a logic diagram or a list of Boolean functions from which a logic diagram can be obtained.
TYPES OF SEQUENTIAL LOGIC CIRCUIT;
As standard logic gates are the building blocks of combinational circuits, bistable latches and flip-flops are the basic building blocks of sequential logic circuits. Sequential logic circuits can be constructed to produce either simple edge-triggered flip-flops or more complex sequential circuits such as storage registers, shift registers, memory devices or counters. Either way sequential logic circuits can be divided into the following three main categories:
- 1. Event Driven – asynchronous circuits that change state immediately when enabled.
- 2. Clock Driven – synchronous circuits that are synchronised to a specific clock signal.
- 3. Pulse Driven – which is a combination of the two that responds to triggering pulses.

As well as the two logic states mentioned above logic level “1” and logic level “0”, a third element is introduced that separates sequential logic circuits from their combinational logic counterparts, namely TIME. Sequential logic circuits return back to their original steady state once reset and sequential circuits with loops or feedback paths are said to be “cyclic” in nature.
We now know that in sequential circuits changes occur only on the application of a clock signal making it synchronous, otherwise the circuit is asynchronous and depends upon an external input. To retain their current state, sequential circuits rely on feedback and this occurs when a fraction of the output is fed back to the input and this is demonstrated as:
SEQUENTIAL LOGIC REPRESENTATION;

The word “Sequential” means that things happen in a “sequence”, one after another and in Sequential Logic circuits, the actual clock signal determines when things will happen next. Simple sequential logic circuits can be constructed from standard Bistable circuits such as: Flip-flops, Latches and Counters and which themselves can be made by simply connecting together universal NAND Gates and/or NOR Gates in a particular combinational way to produce the required sequential circuit.
EXAMPLES OF SEQUENTIAL LOGIC CIRCUITS;
Clocks
State changes of most sequential circuits occur at times specified by free-running clock signals. As the name implies, sequential logic circuits require a means by which events can be sequenced.

The state changes are controlled by the clocks. A “clock” is a special circuit that sends pulses with accurate pulse width and an accurate interval between the consecutive pulses. The interval between consecutive pulses is called the clock cycle time. The Clock speed is normally measured in Megahertz or Gigahertz.
FILP-FLOPS;
The basic building block of the combinational circuit has logic gates, while indeed the basic building block of a sequential circuit is a flip-flop. Flip-flop has a better and greater usage in shift register, counters and memory devices. It is a storage device capable of storing one bit of data. Flip flop has two inputs and two outputs labeled as Q and Q’. It is normal and complements.

BI-STABLES;
In most cases, the bi-stables are indicated by a box or circle. Lines in or around bi-stables not only mark them as bi-stables but also indicate how they function. Bi-stables are of two types latch and flip flop. The bi-stables have two stable states one is SET and the other one is RESET. They can retain either of these stages indefinitely, which makes them useful for storage purposes. Latches and flip-flops are different in the way they change from one state to another.

COUNTERS;
A counter is a register that goes throughout a predetermined sequence of states upon the application of clock pulses. From another viewpoint, a counter is some sort of sequential circuit whose state diagram is a single cycle. In other words, counters are a particular case of a finite state machine. The output is generally a state value.

There are two types of counters: Asynchronous counters (Ripple counter) and the other one is Synchronous counters. The asynchronous counter is the clock signal (CLK), which is simply used to clock the first FF. Each FF (except the first FF) is clocked by the preceding FF. The synchronous counter is the clock signal (CLK) that is functional to all FF, which means that all FF shares the same clock signal. Thus, the output changes at the same time.
REGISTERS;
Registers are clocked sequential circuits. A register is a collection of flip-flops; each flip-flop is capable of storing one bit of information. An n-bit register consists of n flip-flops and is capable of storing n bits of information. Besides flip-flops, a register usually contains a combinational logic to perform some simple tasks. The flip-flops hold binary information. The gates to determine how the information is shifted into the register. Counters are a special type of register. A counter goes through a predetermined sequence of states.

MEMORIES;
Memory elements can be anything that creates a past value available at some future time-devices that can behold a binary value. Memory elements are typically flip-flops. Memory output which is considered as a circuit’s “current state” is a numerical label. The state embodies all the information about the past needed to define the current output.
SEQUENTIAL FEEDBACK LOOP;

The two inverters or NOT gates are connected in series with the output at Q fed back to the input. Unfortunately, this configuration never changes state because the output will always be the same, either a “1” or a “0”, it is permanently set. However, we can see how feedback works by examining the most basic sequential logic components, called the SR flip-flop.
SR FLIP-FLOP;
The SR flip-flop, also known as a SR Latch, can be considered as one of the most basic sequential logic circuit possible. This simple flip-flop is basically a one-bit memory bistable device that has two inputs, one which will “SET” the device (meaning the output = “1”), and is labelled S and one which will “RESET” the device (meaning the output = “0”), labelled R.
Then the SR description stands for “Set-Reset”. The reset input resets the flip-flop back to its original state with an output Q that will be either at a logic level “1” or logic “0” depending upon this set/reset condition.
A basic NAND gate SR flip-flop circuit provides feedback from both of its outputs back to its opposing inputs and is commonly used in memory circuits to store a single data bit. Then the SR flip-flop actually has three inputs, Set, Reset and its current output Q relating to it’s current state or history. The term “Flip-flop” relates to the actual operation of the device, as it can be “flipped” into one logic Set state or “flopped” back into the opposing logic Reset state.
THE NAND GATE SR FLIP-FLOP;
The simplest way to make any basic single bit set-reset SR flip-flop is to connect together a pair of cross-coupled 2-input NAND gates as shown, to form a Set-Reset Bistable also known as an active LOW SR NAND Gate Latch, so that there is feedback from each output to one of the other NAND gate inputs. This device consists of two inputs, one called the Set, S and the other called the Reset, R with two corresponding outputs Q and its inverse or complement Q (not-Q) as shown below.
THE BASIC SR FLIP-FLOP;

THE SET STATE;
Consider the circuit shown above. If the input R is at logic level “0” (R = 0) and input S is at logic level “1” (S = 1), the NAND gate Y has at least one of its inputs at logic “0” therefore, its output Q must be at a logic level “1” (NAND Gate principles). Output Q is also fed back to input “A” and so both inputs to NAND gate X are at logic level “1”, and therefore its output Q must be at logic level “0”.
Again NAND gate principals. If the reset input R changes state, and goes HIGH to logic “1” with S remaining HIGH also at logic level “1”, NAND gate Y inputs are now R = “1” and B = “0”. Since one of its inputs is still at logic level “0” the output at Q still remains HIGH at logic level “1” and there is no change of state. Therefore, the flip-flop circuit is said to be “Latched” or “Set” with Q = “1” and Q = “0”.
RESET STATE;
In this second stable state, Q is at logic level “0”, (not Q = “0”) its inverse output at Q is at logic level “1”, (Q = “1”), and is given by R = “1” and S = “0”. As gate X has one of its inputs at logic “0” its output Q must equal logic level “1” (again NAND gate principles). Output Q is fed back to input “B”, so both inputs to NAND gate Y are at logic “1”, therefore, Q = “0”.
If the set input, S now changes state to logic “1” with input R remaining at logic “1”, output Q still remains LOW at logic level “0” and there is no change of state. Therefore, the flip-flop circuits “Reset” state has also been latched and we can define this “set/reset” action in the following truth table.
TRUTH TABLE FOR THIS SET-RESET FUNCTION;
| State | S | R | Q | Q | Description |
| Set | 1 | 0 | 0 | 1 | Set Q » 1 |
| 1 | 1 | 0 | 1 | no change | |
| Reset | 0 | 1 | 1 | 0 | Reset Q » 0 |
| 1 | 1 | 1 | 0 | no change | |
| Invalid | 0 | 0 | 1 | 1 | Invalid Condition |
It can be seen that when both inputs S = “1” and R = “1” the outputs Q and Q can be at either logic level “1” or “0”, depending upon the state of the inputs S or R BEFORE this input condition existed. Therefore the condition of S = R = “1” does not change the state of the outputs Q and Q.
However, the input state of S = “0” and R = “0” is an undesirable or invalid condition and must be avoided. The condition of S = R = “0” causes both outputs Q and Q to be HIGH together at logic level “1” when we would normally want Q to be the inverse of Q. The result is that the flip-flop looses control of Q and Q, and if the two inputs are now switched “HIGH” again after this condition to logic “1”, the flip-flop becomes unstable and switches to an unknown data state based upon the unbalance as shown in the following switching diagram.
S-R FLIP-FLOP SWITCHING DIAGRAMS;

This unbalance can cause one of the outputs to switch faster than the other resulting in the flip-flop switching to one state or the other which may not be the required state and data corruption will exist. This unstable condition is generally known as its Meta-stable state.
Then, a simple NAND gate SR flip-flop or NAND gate SR latch can be set by applying a logic “0”, (LOW) condition to its Set input and reset again by then applying a logic “0” to its Reset input. The SR flip-flop is said to be in an “invalid” condition (Meta-stable) if both the set and reset inputs are activated simultaneously.
As we have seen above, the basic NAND gate SR flip-flop requires logic “0” inputs to flip or change state from Q to Q and vice versa. We can however, change this basic flip-flop circuit to one that changes state by the application of positive going input signals with the addition of two extra NAND gates connected as inverters to the S and R inputs as shown.
POSITIVE NAND GATE SR FLIP-FLOP;

As well as using NAND gates, it is also possible to construct simple one-bit SR Flip-flops using two cross-coupled NOR gates connected in the same configuration. The circuit will work in a similar way to the NAND gate circuit above, except that the inputs are active HIGH and the invalid condition exists when both its inputs are at logic level “1”, and this is shown below.
THE NOR GATE SR FLIP-FLOP;

SWITCH DEBOUNCE CIRCUITS;
Edge-triggered flip-flops require a nice clean signal transition, and one practical use of this type of set-reset circuit is as a latch used to help eliminate mechanical switch “bounce”. As its name implies, switch bounce occurs when the contacts of any mechanically operated switch, push-button or keypad are operated and the internal switch contacts do not fully close cleanly, but bounce together first before closing (or opening) when the switch is pressed.
This gives rise to a series of individual pulses which can be as long as tens of milliseconds that an electronic system or circuit such as a digital counter may see as a series of logic pulses instead of one long single pulse and behave incorrectly. For example, during this bounce period the output voltage can fluctuate wildly and may register multiple input counts instead of one single count. Then set-reset SR Flip-flops or Bistable Latch circuits can be used to eliminate this kind of problem and this is demonstrated below.
SR FLIP FLOP SWITCH DEBOUNE CIRCUIT;

Depending upon the current state of the output, if the set or reset buttons are depressed the output will change over in the manner described above and any additional unwanted inputs (bounces) from the mechanical action of the switch will have no effect on the output at Q.
When the other button is pressed, the very first contact will cause the latch to change state, but any additional mechanical switch bounces will also have no effect. The SR flip-flop can then be RESET automatically after a short period of time, for example 0.5 seconds, so as to register any additional and intentional repeat inputs from the same switch contacts, such as multiple inputs from a keyboards “RETURN” key.
Commonly available IC’s specifically made to overcome the problem of switch bounce are the MAX6816, single input, MAX6817, dual input and the MAX6818 octal input switch debouncer IC’s. These chips contain the necessary flip-flop circuitry to provide clean interfacing of mechanical switches to digital systems.
Set-Reset bistable latches can also be used as Monostable (one-shot) pulse generators to generate a single output pulse, either high or low, of some specified width or time period for timing or control purposes. The 74LS279 is a Quad SR Bistable Latch IC, which contains four individual NAND type bistable’s within a single chip enabling switch debounce or monostable/astable clock circuits to be easily constructed.
QUAD SR BISTABLE LATCH 74LS279;

GATED OR CLOCKED SR FLIP-FLOP;
It is sometimes desirable in sequential logic circuits to have a bistable SR flip-flop that only changes state when certain conditions are met regardless of the condition of either the Set or the Reset inputs. By connecting a 2-input AND gate in series with each input terminal of the SR Flip-flop a Gated SR Flip-flop can be created. This extra conditional input is called an “Enable” input and is given the prefix of “EN“. The addition of this input means that the output at Q only changes state when it is HIGH and can therefore be used as a clock (CLK) input making it level-sensitive as shown below.
GATED SR FLIP-FLOP;

When the Enable input “EN” is at logic level “0”, the outputs of the two AND gates are also at logic level “0”, (AND Gate principles) regardless of the condition of the two inputs S and R, latching the two outputs Q and Q into their last known state. When the enable input “EN” changes to logic level “1” the circuit responds as a normal SR bistable flip-flop with the two AND gates becoming transparent to the Set and Reset signals.
This additional enable input can also be connected to a clock timing signal (CLK) adding clock synchronisation to the flip-flop creating what is sometimes called a “Clocked SR Flip-flop“. So a Gated Bistable SR Flip-flop operates as a standard bistable latch but the outputs are only activated when a logic “1” is applied to its EN input and deactivated by a logic “0”.
In the next tutorial about Sequential Logic Circuits, we will look at another type of simple edge-triggered flip-flop which is very similar to the RS flip-flop called a JK Flip-flop named after its inventor, Jack Kilby. The JK flip-flop is the most widely used of all the flip-flop designs as it is considered.
MORE DETAILS;
https://youtu.be/E_oo6TAY-dA
OR
*****************************************************
Comments
Post a Comment