Skip to main content

LOGIC GATES

 LOGIC GATES

                      In digital electronics, the decision making capability of the gate circuit is called logic, and a type of logic circuit that performs a specific logical operation e.g AND or OR etc is called a gate. So, the logic gates are the type of electronic circuits that makes logical decisions, and their output depends on the preset rules. The logic gates can have multiple inputs but always has a single output. A gate is just like a switch which can be ON or OFF. The ON state represents logic 1, while the OFF state represents logic 0. A gate can not only add, subtract, count, etc but can also store the information. 


The most common types of the gates;

                                      In Boolean Algebra, there are three basic operations, +,\:.\:,\:^\prime which are analogous to disjunction, conjunction, and negation in propositional logic. Each of these operations has a corresponding logic gate. Apart from these there are a few other logic gates as well.

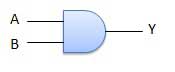
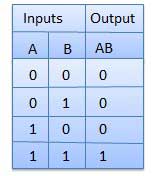
  • AND gate (.)– The AND gate gives an output of 1 if both the two inputs are 1, it gives 0 otherwise.
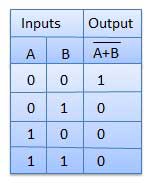
  • OR gate(+) – The OR gate gives an output of 1 if either of the two inputs are 1, it gives 0 otherwise.
  • NOT gate(‘) – The NOT gate gives an output of 1 input is 0 and vice-versa.
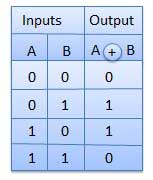
  • XOR gate(\oplus) – The XOR gate gives an output of 1 if either both inputs are different, it gives 0 if they are same.
  • NAND gate(\uparrow)- The NAND gate (negated AND) gives an output of 0 if both inputs are 1, it gives 1 otherwise.
  • NOR gate(\downarrow)- The NOR gate (negated OR) gives an output of 1 if both inputs are 0, it gives 0 otherwise.
  • XNOR gate(\odot)- The XNOR gate (negated XOR) gives an output of 1 both inputs are same and 0 if both are different.                                                                                                                                                                                                                                        LOGIC GATE SYMBOLS 
    Small Logic Gates — The building blocks of digital circuits -  Part 2


                                              1.AND GATE;

               A circuit which performs an AND operation is shown in figure. It has n input (n >= 2) and one output.


AND gate

Logic diagram;

AND Logical Diagram

Truth Table;

AND Truth Table


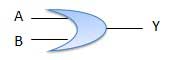
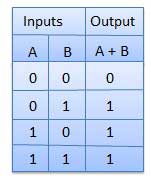
                      2.OR GATE;

             A circuit which performs an OR operation is shown in figure. It has n input (n >= 2) and one output.


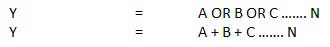
OR gate

LOGIC DIAGRAM;

OR Logical Diagram

TRUTH TABLE;

OR Truth Table


                        3.NOT GATE;

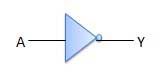
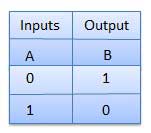
          NOT gate is also known as Inverter. It has one input A and one output Y.

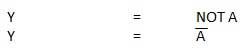
NOT gate

LOGIC DIAGRAM;

NOT Logical Diagram

TRUTH TABLE;

NOT Truth Table


                          4. NAND GATE;

A NOT-AND operation is known as NAND operation. It has n input (n >= 2) and one output.


NAND gate

LOGIC DIAGRAM;


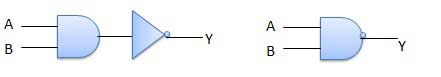
NAND Logical Diagram

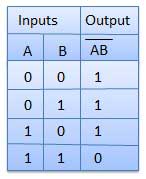
TRUTH TABLE;

NAND Truth Table

                             5.NOR GATE;

A NOT-OR operation is known as NOR operation. It has n input (n >= 2) and one output.


NOR gate

LOGIC DIAGRAM;


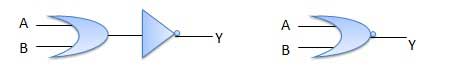
NOR Logical Diagram

TRUTH TABLE;

NOR Truth Table

                            6. XOR GATE;

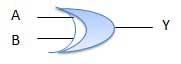
XOR or Ex-OR gate is a special type of gate. It can be used in the half adder, full adder and subtractor. The exclusive-OR gate is abbreviated as EX-OR gate or sometime as X-OR gate. It has n input (n >= 2) and one output.


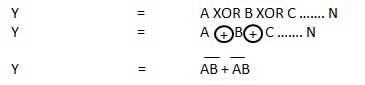
XOR gate

LOGIC GATE;

XOR Logical Diagram

TRUTH TABLE;

XOR Truth Table

                          7. XNOR GATE;

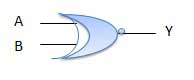
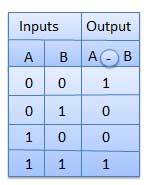
XNOR gate is a special type of gate. It can be used in the half adder, full adder and subtractor. The exclusive-NOR gate is abbreviated as EX-NOR gate or sometime as X-NOR gate. It has n input (n >= 2) and one output.


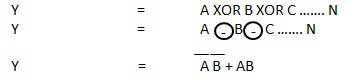
XNOR gate

LOGIC DIAGRAM;

XNOR Logical Diagram

TRUTH TABLE;

XNOR Truth Table

                       MORE DETAILS;

             https://youtu.be/WT1NJrw0Aao

                                  OR




Comments

Post a Comment

Popular posts from this blog

NUMBER SYSTEM CONVERSION

NUMBER BASE CONVERSION                     In our previous section, we learned different types of number systems such as binary, decimal, octal, and hexadecimal. In this part of the tutorial, we will learn how we can change a number from one number system to another number system. As, we have four types of number systems so each one can be converted into the remaining three systems. There are the following conversions possible in Number System Binary to other Number Systems. Decimal to other Number Systems. Octal to other Number Systems. Hexadecimal to other Number Systems.                                                                                                          ...
Post a Comment
Read more

CONONICAL FORMS (SOP AND POS)

  CONONICAL FORMS The use of switching devices like transistors give rise to a special case of the Boolean algebra called as switching algebra. In switching algebra, all the variables assume one of the two values which are 0 and 1. In Boolean algebra, 0 is used to represent the ‘open’ state or ‘false’ state of logic gate. Similarly, 1 is used to represent the ‘closed’ state or ‘true’ state of logic gate. A Boolean expression is an expression which consists of variables, constants (0-false and 1-true) and logical operators which results in true or false. TWO TYPE OF CONONICAL FORMS; A Boolean function is an algebraic form of Boolean expression. A Boolean function of n-variables is represented by f(x1, x2, x3….xn). By using Boolean laws and theorems, we can simplify the Boolean functions of digital circuits. A brief note of different ways of representing a Boolean function is shown below. Sum-of-Products (SOP) Form Product-of-sums (POS) form Canonical forms There are two types of can...
Post a Comment
Read more

BINARY ARITHMETIC

 BINARY ARITHMETIC                         Binary arithmetic  is used in digital systems mainly because the numbers (decimal and floating-point numbers) are stored in  binary  format in most computer systems. All  arithmetic  operations such as addition, subtraction, multiplication, and division are done in  binary  representation of numbers.       1) BINARY ADDITION; Binary Addition   It is a key for  binary  subtraction, multiplication, division. There are  four rules of  binary addition .  In fourth case, a  binary addition  is creating a sum of (1 + 1 = 10) i.e. 0 is written in the given column and a carry of 1 over to the next column.     Basic  arithmetic  operations like  addition , subtraction, multiplication, and division, play  an important role in mathematics .        ...
Post a Comment
Read more