Skip to main content

BOOLEN ALGEBRA

 BOOLEN ALGEBRA 

                    George Boole, (born November 2, 1815, Lincoln, Lincolnshire, England—died December 8, 1864, Ballintemple, County Cork, Ireland), English mathematician who helped establish modern symbolic logic and whose algebra of logic, now called Boolean algebra, is basic to the design of digital computer circuits.

                     


 INTRODUTION;

The most obvious way to simplify Boolean expressions is to manipulate them in the same way as normal algebraic expressions are manipulated. With regards to logic relations in digital forms, a set of rules for symbolic manipulation is needed in order to solve for the unknowns.
A set of rules formulated by the English mathematician George Boole describe certain propositions whose outcome would be either true or false. With regard to digital logic, these rules are used to describe circuits whose state can be either, 1 (true) or 0 (false). In order to fully understand this, the relation between the AND gate, OR gate and NOT gate operations should be appreciated. A number of rules can be derived from these relations as Table 1 demonstrates.
  • P1: X = 0 or X = 1
  • P2: 0 . 0 = 0
  • P3: 1 + 1 = 1
  • P4: 0 + 0 = 0
  • P5: 1 . 1 = 1
  • P6: 1 . 0 = 0 . 1 = 0
  • P7: 1 + 0 = 0 + 1 = 1

 BOOLEAN ALGEBRA OPERATIONS;


The basic operations of Boolean algebra are as follows:

  • Conjunction or AND operation
  • Disjunction or OR operation
  • Negation or Not operation

Boolean Algebra

 

Below is the table defining the symbols for all three basic operations.

OperatorSymbolPrecedence
NOT‘ (or) ¬Highest
AND. (or) ∧Middle
OR+ (or) ∨Lowest

Suppose A and B are two boolean variables, then we can define the three operations as;

  • A conjunction B or A AND B, satisfies A ∧ B = True, if A = B = True or else A ∧ B = False.
  • A disjunction B or A OR B, satisfies A ∨ B = False, if A = B = False, else A ∨ B = True.
  • Negation A or ¬A satisfies ¬A = False, if A = True and ¬A = True if A = False                                                                                                        
BOOLEN ALGEBRA TERMINOLOGIES;

                    Now, let us discuss the important terminologies covered in Boolean algebra.

Boolean Algebra: Boolean algebra is the branch of algebra that deals with logical operations and binary variables.

Boolean Variables: A boolean variable is defined as a variable or a symbol defined as a variable or a symbol, generally an alphabet that represents the logical quantities such as 0 or 1.

Boolean Function: A boolean function consists of binary variables, logical operators, constants such as 0 and 1, equal to the operator, and the parenthesis symbols.

Literal: A literal may be a variable or a complement of a variable.

Complement: The complement is defined as the inverse of a variable, which is represented by a bar over the variable.

Truth Table: The truth table is a table that gives all the possible values of logical variables and the combination of the variables. It is possible to convert the boolean equation into a truth table. The number of rows in the truth table should be equal to 2n, where “n” is the number of variables in the equation. For example, if a boolean equation consists of 3 variables, then the number of rows in the truth table is 8. (i.e.,) 23 = 8.

 

BOOLEN ALGEBRA TRUTH TABLE;


Boolean
Expression		DescriptionEquivalent
Switching Circuit		Boolean Algebra
Law or Rule
A + 1 = 1A in parallel with
closed = “CLOSED”		universal parallel circuitAnnulment
A + 0 = AA in parallel with
open = “A”		universal parallelIdentity
A . 1 = AA in series with
closed = “A”		universal series circuitIdentity
A . 0 = 0A in series with
open = “OPEN”		universal seriesAnnulment
A + A = AA in parallel with
A = “A”		idempotent parallel circuitIdempotent
A . A = AA in series with
A = “A”		idempotent series circuitIdempotent
NOT A = ANOT NOT A
(double negative) = “A”		 Double Negation
A + A = 1A in parallel with
NOT A = “CLOSED”		complement parallel circuitComplement
A . A = 0A in series with
NOT A = “OPEN”		complement series circuitComplement
A+B = B+AA in parallel with B =
B in parallel with A		absorption parallel circuitCommutative
A.B = B.AA in series with B =
B in series with A		absorption series circuitCommutative
A+B = A.Binvert and replace OR with AND de Morgan’s Theorem
A.B = A+Binvert and replace AND with OR de Morgan’s Theorem

    

BOOLEN ALGEBRA RULES;                                                                                                                      Following are the important rules used in Boolean algebra.

  • Variable used can have only two values. Binary 1 for HIGH and Binary 0 for LOW.
  • The complement of a variable is represented by an overbar. Thus, complement of variable B is represented as B¯. Thus if B = 0 then B¯=1 and B = 1 then B¯ = 0.
  • OR-ing of the variables is represented by a plus (+) sign between them. For example OR-ing of A, B, C is represented as A + B + C.
  • Logical AND-ing of the two or more variable is represented by writing a dot between them such as A.B.C. Sometimes the dot may be omitted like ABC.

Related Links

Truth TableTautology
ConjunctionMathematical Logic


LAWS OF BOOLEN ALGEBRA;   

  

                               The variables used in Boolean Algebra only have one of two possible values, a logic “0” and a logic “1” but an expression can have an infinite number of variables all labelled individually to represent inputs to the expression, For example, variables A, B, C etc, giving us a logical expression of A + B = C, but each variable can ONLY be a 0 or a 1.

Examples of these individual laws of Boolean, rules and theorems for Boolean Algebra are given in the following table.

There are six types of Boolean algebra laws. They are:

  • Commutative law
  • Associative law
  • Distributive law
  • AND law
  • OR law
  • Inversion law

Those six laws are explained in detail here.


                           1.COMMUTATIVE LAW;


                             Any binary operation which satisfies the following expression is referred to as a commutative operation. Commutative law states that changing the sequence of the variables does not have any effect on the output of a logic circuit.

  • A. B = B. A
  • A + B = B + A

Boolean Algebra and Logic Simplification. Boolean Addition & Multiplication Boolean Addition performed by OR gate Sum Term describes Boolean Addition. - ppt download


2.ASSOCIATIVE LAW;

                          It states that the order in which the logic operations are performed is irrelevant as their effect is the same.

  • ( A. B ). C = A . ( B . C )
  • ( A + B ) + C = A + ( B + C)
PPT ON BOOLEAN ALGEBRA - PowerPoint Slides
3.DISTRIBUTIVE LAW;

                          Distributive law states the following conditions:

                     .   A. ( B + C) = (A. B) + (A. C)

                     .   A + (B. C) = (A + B) . ( A + C)


                                                          Basic gates and boolean algebra

                           

                   

                       4.AND LAW;

These laws use the AND operation. Therefore they are called as AND laws.

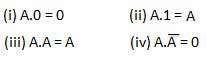
AND Law


                                  5.OR LAW;

These laws use the OR operation. Therefore they are called as OR laws.

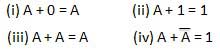
OR Law

                               

                                6. INVERSION LAW;

This law uses the NOT operation. The inversion law states that double inversion of a variable results in the original variable itself.

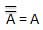
NOT Law





MORE DATAILS;

https://youtu.be/62dCbxwci8c


Comments

Post a Comment

Popular posts from this blog

NUMBER SYSTEM CONVERSION

NUMBER BASE CONVERSION                     In our previous section, we learned different types of number systems such as binary, decimal, octal, and hexadecimal. In this part of the tutorial, we will learn how we can change a number from one number system to another number system. As, we have four types of number systems so each one can be converted into the remaining three systems. There are the following conversions possible in Number System Binary to other Number Systems. Decimal to other Number Systems. Octal to other Number Systems. Hexadecimal to other Number Systems.                                                                                                          ...
Post a Comment
Read more

SEQUENTIAL GATES

 SEQUENTIAL GATES INTRODUCTION;                      A Sequential  logic circuits  is a form of the binary circuit; its design employs one or more inputs and one or more outputs, whose states are related to some definite rules that depend on previous states. Both the inputs and outputs can reach either of the two states: logic 0 (low) or logic 1 (high). In these circuits, their output depends, not only on the combination of the logic states at its inputs but moreover on the logic states that existed previously. In other words, their output depends on a SEQUENCE of the events occurring at the circuit inputs. Examples of such circuits include clocks, flip-flops, bi-stables, counters, memories, and registers. The actions of the circuits depend on the range of basic sub-circuits. SEQUENTIONAL LOGIC CIRCUIT;                            Sequential Logic C...
Post a Comment
Read more

CONONICAL FORMS (SOP AND POS)

  CONONICAL FORMS The use of switching devices like transistors give rise to a special case of the Boolean algebra called as switching algebra. In switching algebra, all the variables assume one of the two values which are 0 and 1. In Boolean algebra, 0 is used to represent the ‘open’ state or ‘false’ state of logic gate. Similarly, 1 is used to represent the ‘closed’ state or ‘true’ state of logic gate. A Boolean expression is an expression which consists of variables, constants (0-false and 1-true) and logical operators which results in true or false. TWO TYPE OF CONONICAL FORMS; A Boolean function is an algebraic form of Boolean expression. A Boolean function of n-variables is represented by f(x1, x2, x3….xn). By using Boolean laws and theorems, we can simplify the Boolean functions of digital circuits. A brief note of different ways of representing a Boolean function is shown below. Sum-of-Products (SOP) Form Product-of-sums (POS) form Canonical forms There are two types of can...
Post a Comment
Read more