KARNAUGH MAP

 KARNAUGH MAP

A Karnaugh map (K-map for short) is a useful tool used in the simplification of combinational boolean equations and the creation of sequential logic circuits. Karnaugh maps were created by Maurice Karnaugh in 1953. The size of a Karnaugh map can be very large, however a size of four columns by four rows is easier to understand than any larger maps.

The philosophy behind these drawings is that differences of only one bit for the logic of a boolean equation are adjacent to each other. This is just an organizational method for a boolean logic truth table, but it can give you the ability to help simplify logical equations. This has proven to be especially useful for digital circuit designers, as it can suggest components which can be eliminated or a way to simplify circuit designs. This reduces both the cost and complexity of these designs, and even an automated method for developing these circuits assuming that you can come up with a logical truth table in the first place.

What is going to be demonstrated here is how to manually evaluate Karnaugh Maps. For very complex circuit designs that involve dozens or even hundreds of variables, there is software available that automates this process.

EXAMPLE;

Karnaugh maps are used to facilitate the simplification of Boolean algebra functions. For example, consider the Boolean function described by the following truth table.

Truth table of a function

	A	B	C	D	${\displaystyle f(A,B,C,D)}$
0	0	0	0	0	0
1	0	0	0	1	0
2	0	0	1	0	0
3	0	0	1	1	0
4	0	1	0	0	0
5	0	1	0	1	0
6	0	1	1	0	1
7	0	1	1	1	0
8	1	0	0	0	1
9	1	0	0	1	1
10	1	0	1	0	1
11	1	0	1	1	1
12	1	1	0	0	1
13	1	1	0	1	1
14	1	1	1	0	1
15	1	1	1	1	0

KARNAUGH MAP;

   

MINIMIZATION WITH KARNAUGH MAPS AND ADVANTAGES OF K-MAP;

• K-maps are used to convert the truth table of a Boolean equation into minimized SOP form.
• Easy and simple basic rules for the simplification.
• The K-map method is faster and more efficient than other simplification techniques of Boolean algebra.
• All rows in the K-map are represented by using a square shaped cells, in which each square in that will represent a minterm.
• It is easy to convert a truth table to k-map and k-map to Sum of Products form equation.

There are 2 forms in converting a Boolean equation into K-map:

1. Un-optimized form
2. Optimized form

• Un-optimized form: It involves in converting the number of 1’s into equal number of product terms (min terms) in an SOP equation.
• Optimized form: It involves in reducing the number of min terms in the SOP equation.

GROUPING OF K-MAP VARIABLES;

• There are some rules to follow while we are grouping the variables in K-maps. They are
• The square that contains ‘1’ should be taken in simplifying, at least once.
• The square that contains ‘1’ can be considered as many times as the grouping is possible with it.
•  Group shouldn’t include any zeros (0).
• A group should be the as large as possible.
• Groups can be horizontal or vertical. Grouping of variables in diagonal manner is not allowed.
• 
  

• If the square containing ‘1’ has no possibility to be placed in a group, then it should be added to the final expression.
• Groups can overlap.
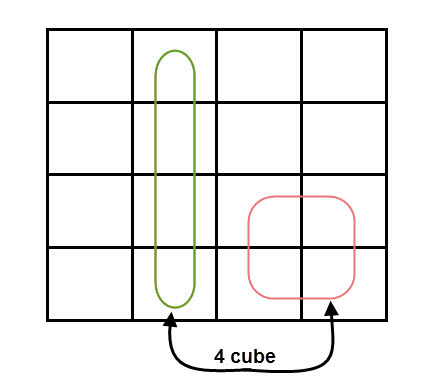
• The number of squares in a group must be equal to powers of 2, such as 1, 2, 4, 8 etc.
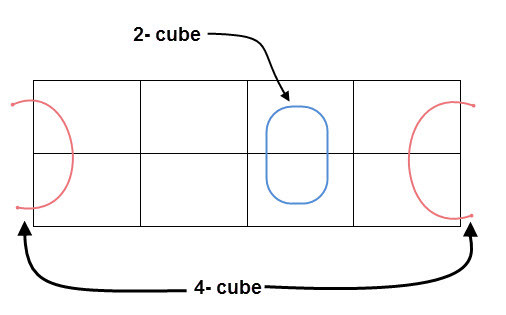
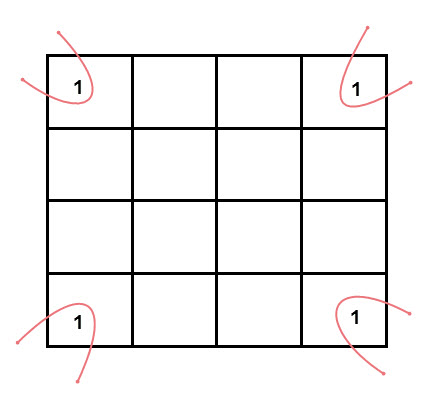
• Groups can wrap around. As the K-map is considered as spherical or folded, the squares at the corners (which are at the end of the column or row) should be considered as they adjacent squares.
• The grouping of K-map variables can be done in many ways, so the obtained simplified equation need not to be unique always.
• The Boolean equation must be in must be in canonical form, in order to draw a K-map.

2 VARIABLE K-MAP;

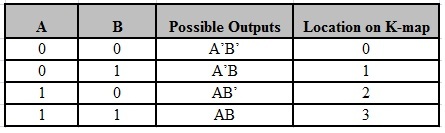
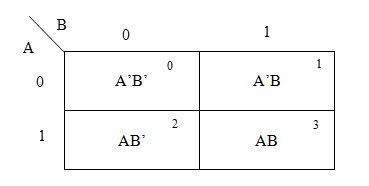
There are 4 cells (22) in the 2-variable k-map. It will look like (see below image)

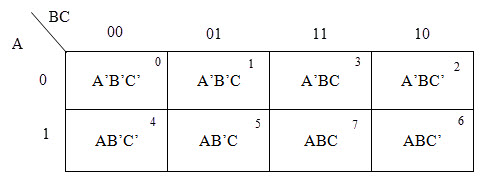
The possible min terms with 2 variables (A and B) are A.B, A.B’, A’.B and A’.B’. The conjunctions of the variables (A, B) and (A’, B) are represented in the cells of the top row and (A, B’) and (A’, B’) in cells of the bottom row. The following table shows the positions of all the possible outputs of 2-variable Boolean function on a K-map.

A general representation of a 2 variable K-map plot is shown below.

 

When we are simplifying a Boolean equation using Karnaugh map, we represent the each cell of K-map containing the conjunction term with 1. After that, we group the adjacent cells with possible sizes as 2 or 4. In case of larger k-maps, we can group the variables in larger sizes like 8 or 16.

The groups of variables should be in rectangular shape, that means the groups must be formed by combining adjacent cells either vertically or horizontally. Diagonal shaped or L-shaped groups are not allowed. The following example demonstrates a K-map simplification of a 2-variable Boolean equation.

EXAMPLE;

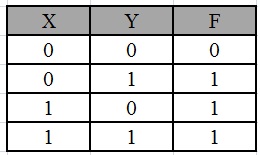
Simplify the given 2-variable Boolean equation by using K-map.

F = X Y’ + X’ Y + X’Y’

First, let’s construct the truth table for the given equation,

We put 1 at the output terms given in equation.

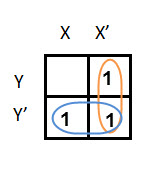
In this K-map, we can create 2 groups by following the rules for grouping, one is by combining (X’, Y) and (X’, Y’) terms and the other is by combining (X, Y’) and (X’, Y’) terms. Here the lower right cell is used in both groups.
After grouping the variables, the next step is determining the minimized expression.

By reducing each group, we obtain a conjunction of the minimized expression such as by taking out the common terms from two groups, i.e. X’ and Y’. So the reduced equation will be X’ +Y’.

3 VARIABLE K-MAP;

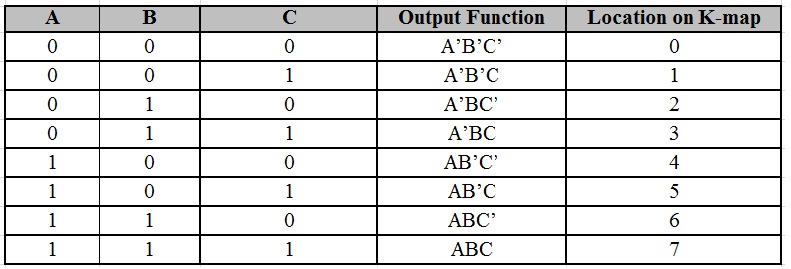
For a 3-variable Boolean function, there is a possibility of 8 output min terms. The general representation of all the min terms using 3-variables is shown below.

A typical plot of a 3-variable K-map is shown below. It can be observed that the positions of columns 10 and 11 are interchanged so that there is only change in one variable across adjacent cells. This modification will allow in minimizing the logic.

Up to 8 cells can be grouped in case of a 3-variable K-map with other possibilities being 1,2 and 4.

EXAMPLE;

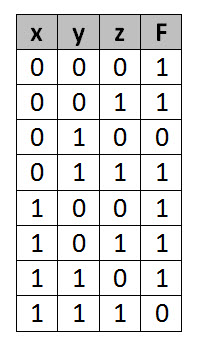
Simplify the given 3-variable Boolean equation by using k-map.

F = X’ Y Z + X’ Y’ Z + X Y Z’ + X’ Y’ Z’ + X Y Z + X Y’ Z’

First, let’s construct the truth table for the given equation,

We put 1 at the output terms given in equation.

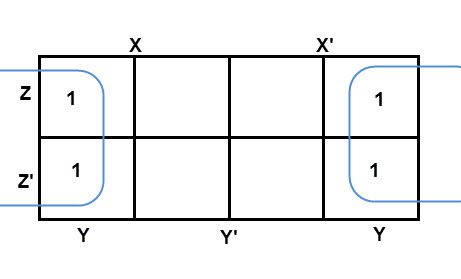
There are 8 cells (23) in the 3-variable k-map. It will look like (see below image).

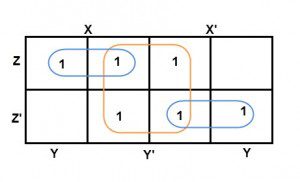
The largest group size will be 8 but we can also form the groups of size 4 and size 2, by possibility. In the 3 variable Karnaugh map, we consider the left most column of the k-map as the adjacent column of rightmost column. So the size 4 group is formed as shown below.

And in both the terms, we have ‘Y’ in common. So the group of size 4 is reduced as the conjunction Y. To consume every cell which has 1 in it, we group the rest of cells to form size 2 group, as shown below.

The 2 size group has no common variables, so they are written with their variables and its conjugates. So the reduced equation will be X Z’ + Y’ + X’ Z. In this equation, no further minimization is possible.

4 VARIABLE K-MAP;

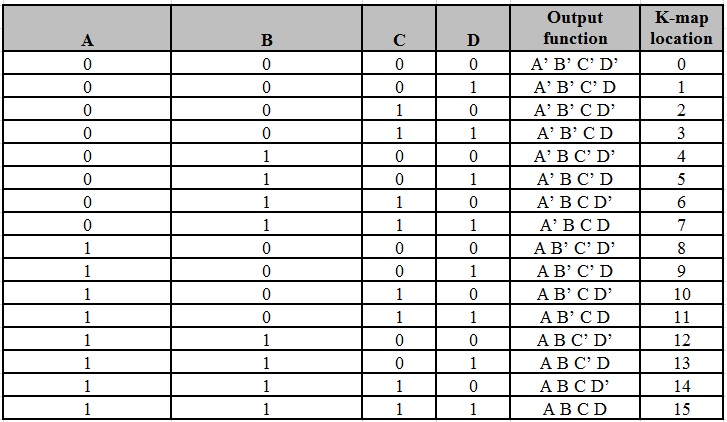
There are 16 possible min terms in case of a 4-variable Boolean function. The general representation of minterms using 4 variables is shown below.

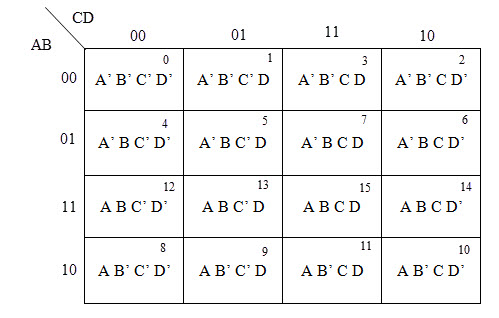
A typical 4-variable K-map plot is shown below. It can be observed that both the columns and rows of 10 and 11 are interchanged.

The possible number of cells that can be grouped together are 1, 2, 4, 8 and 16.

EXAMPLE;

Simplify the given 4-variable Boolean equation by using k-map. F (W, X, Y, Z) = (1, 5, 12, 13)

Sol: F (W, X, Y, Z) = (1, 5, 12, 13)

By preparing k-map, we can minimize the given Boolean equation as

F = W Y’ Z + W ‘Y’ Z

MORE DETAILS;

https://youtu.be/bISJOMo_pH8

OR